Nem-lineáris számítások konvergenciája

Konvergencia & Divergencia #

A nemlineáris számítás iteratív számítás. A “konvergencia” kifejezés azt a tulajdonságot jelenti, hogy az eredmények minden iterációs lépéssel egy bizonyos (új) értéket kapnak. Ha nem így történik (az eredmények váltakoznak, vagy növekvő eltéréseket mutatnak az előző iterációs lépéshez képest), akkor a rendszer “divergenciának” nevezi. Ezekben az esetekben a számítás nem fog befejeződni, nem kapunk eredményt.

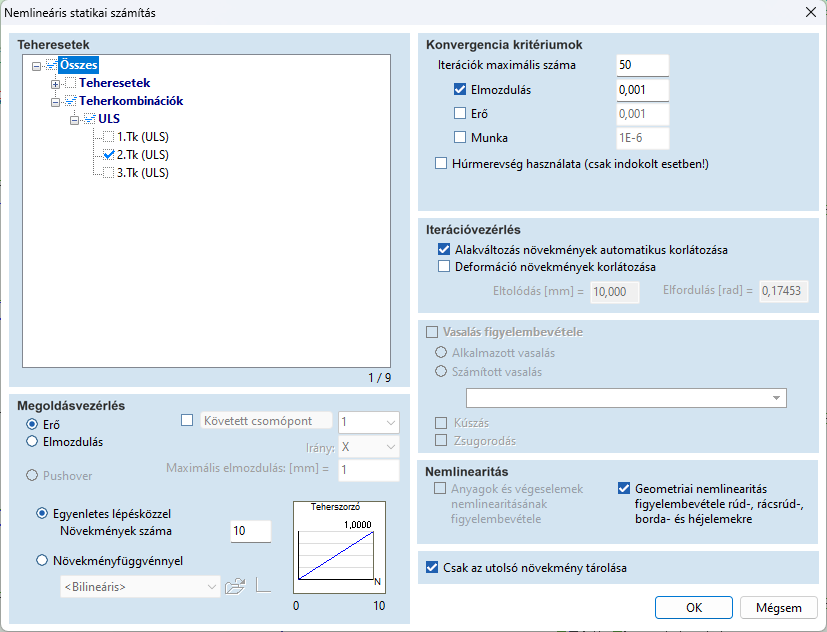
A konvergencia kritériumai a nemlineáris számítások paramétereiben állíthatók be. A legtöbb esetben ajánlott az elmozdulásokat használni konvergenciakritériumként. A konvergenciakritériumok értékét csak a számítási eljárás alapos megértésével szabad módosítani, mivel az nem csak az iterációs lépések szükséges számát (és ezáltal a számítási időt), hanem az eredmények pontosságát is befolyásolja.

A számítás során a konvergencia viselkedése az “Iterációk” alatt tekinthető meg. A számítás után a “modellinformációk” alatt tekinthető meg (függőleges eszköztár, balra).

A konvergencia akkor teljesül, ha a választott kritériumunk görbéje (félkövérrel szedve) nulla alá csökken.

Ha a görbe nem ér be a nulla alá, akkor divergenciát feltételezünk.

 

• • A görbe csökken, de nem nulla alá

• • A görbe (többé-kevésbé) állandó

• • A görbe egy bizonyos érték körül váltakozik

• • A görbe emelkedik (egy bizonyos növekmény után)

A divergenciákat különböző okokból eredhetnek. A megfelelő lépések a modell felépítése és a konvergenciagörbe alapján határozhatók meg.

Stabilitás nem-lineáris körülmények között #

A nemlineáris számításban instabilitások fordulhatnak elő, még akkor is, ha a modell lineáris körülmények között stabil.

 

• • A nemlineáris elemtulajdonságok megakadályozzák az egyensúlyt (lásd a jobb oldali példát)

• • A nagy terhelés folyamatosan növekvő deformációkhoz vezet (pl. az oszlopok kihajlanak)

A nemlineáris instabilitások a konvergenciagörbe helytelen viselkedését okozhatják, és hibát a számítás végén. Bizonyos esetekben a számítás elvégezhető, de az eredmények egyértelműen sértik a nemlineáris elemek tulajdonságait (pl. húzóerő egy támaszban, ahol korábban ki volt zárva a húzás).

Iterációk maximális száma #

Ha a konvergenciagörbe csökken, viszont nem éri el a nullát, feltételezhető, hogy a számítás konvergál, de nagyobb számú iterációs lépésre van szükség. Ezekben az esetekben a “maximális iterációk” nagyobb értékre állíthatók a nemlineáris számítás paraméterei között. Megjegyzés | a maximális iterációk csökkentése konvergens rendszerek esetén csak akkor csökkenti a számítási időt, ha a számítás nem konvergál a kritériumokhoz, mivel a számítás automatikusan leáll, ha a konvergenciakritériumok teljesülnek. Még akkor is, ha ez azt jelenti, hogy kevesebb iteráció kerül kiszámításra, mint amit megadtunk.

Húrmerevség #

A képlékeny csuklók váltakozó viselkedést okozhatnak a kezdeti képlékenyedés körül. A konvergenciagörbe egy állandó (pozitív) érték körül fog váltakozik.

Első lépésként meg kell próbálni a számítást megnövekedett számú (egyenlő) növekményekkel futtatni (pl. 30, 50, 100). Ha ez nem vezet konvergenciához, akkor a “Húrmerevség használata” opció bekapcsolása megoldás lehet. Ennek során növelni kell a maximális iterációk számát (> 100), mivel ezek a számítások általában lassan konvergálnak. Bizonyos esetekben a felhasználó által definiált “növekményfüggvény” (lásd alább) használata sikeres számításhoz vezethet.

Növekmények száma & Növekmény függvény #

Ha a divergenciát geometriai nemlinearitások (nagy deformációk az egyes növekményekben) okozzák, akkor alkalmazhatunk egy, a felhasználó által definiált növekményfüggvényt a számítás futtatásához. Első lépésként megnövekedett számú “egyenlő növekményt” (lineáris növekményfüggvényt) kell használni, mivel egy megfelelő növekményfüggvény kifejlesztése meglehetősen időigényes lehet.

A növekmény függvényt a “növekményfüggvény-szerkesztő” táblázatában található töréspontok sorozata határozza meg. Az értékek automatikusan az N növekményszám szerint vannak rendezve.

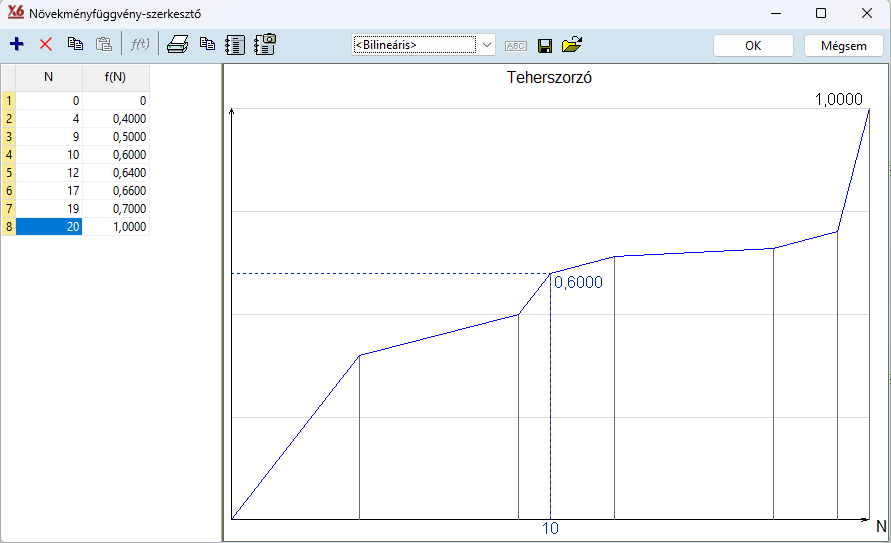
A nemlineáris anyag- és/vagy elemtulajdonságok figyelembevételéhez a növekményfüggvénynek folyamatosan emelkednie kell (nincsenek vízszintes vagy leszálló szakaszok).

A geometriai nem-linearitások kiszámítása (a deformáció hatása az igénybevételekre) bármilyen növekményfüggvénnyel elvégezhető.

A növekményfüggvény előállítása #

Az alábbiakban ismertetett mindkét eljárásban találhatóak azonos elvek.

 

• • Iteratív eljárás több számítási futtatással

• • Számítás megnövekedett számú “egyenlő növekménnyel” első lépésként

• • A növekményfüggvény módosítása az utolsó konvergáló növekmény és a görbe vége között (nem konvergáló növekmények módosítása az elején)

• • Maximális terhelési tényező 1,0 (a teljes terhelést figyelembe kell venni)

• • A töréspontokat csak akkor veszünk fel, ha korábban még nem léteztek

Egyszerű eljárás

A divergáló és az azt követő növekmények felosztása

 

• • Kisebb erőforrásigény (kisebb számú számítási futtatás szükséges)

• • Több növekmény (nagyobb számítási idő)

Optimalizált eljárás

A divergáló növekmény felosztása a következő növekmények módosítása nélkül

 

• • Nagyobb erőforrásigény (nagyobb számú számítási futtatás szükséges)

• • Kevesebb növekmény (kisebb számítási idő)